6.4.4.10. 계절적인 데이터에 대한 박스-젠킨스 분석
November 25, 2016
시계열 G 이 예제에서는 Box, Jenkins, and Reinsel 1994에 있는 시계열 데이터 G를 사용하여 계절적인 데이터에 대한 박스-젠킨스 시계열 분석 방법을 다룰 것이다. 아래 그림에서 볼 수 있듯이 144개의 관측값이 있다.
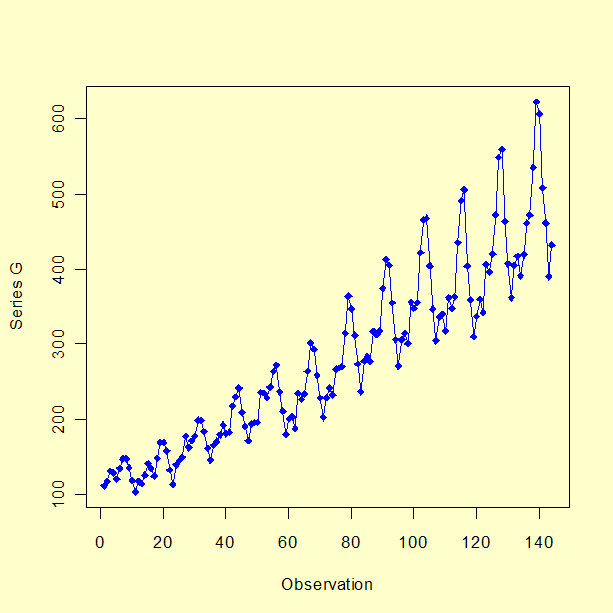
자연 로그 변환으로 일정하지 않은 분산 효과를 없앨 수 있다.
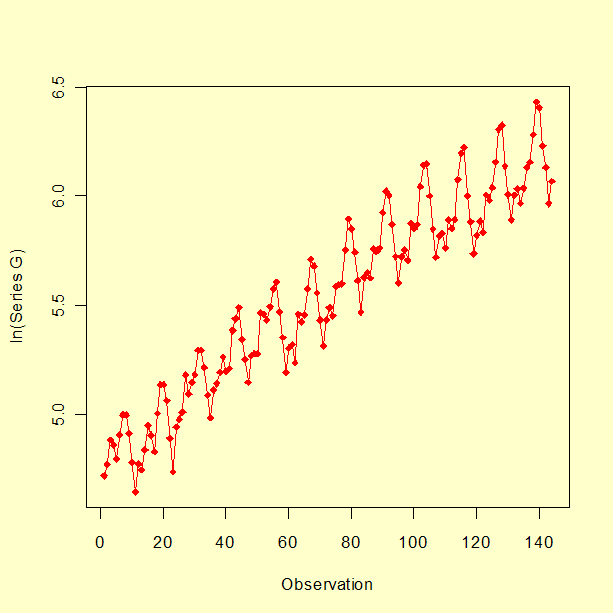
그 다음, 뺄셈으로 시계열에서 추세를 없앤다. 결과 시계열은 다음과 같다.
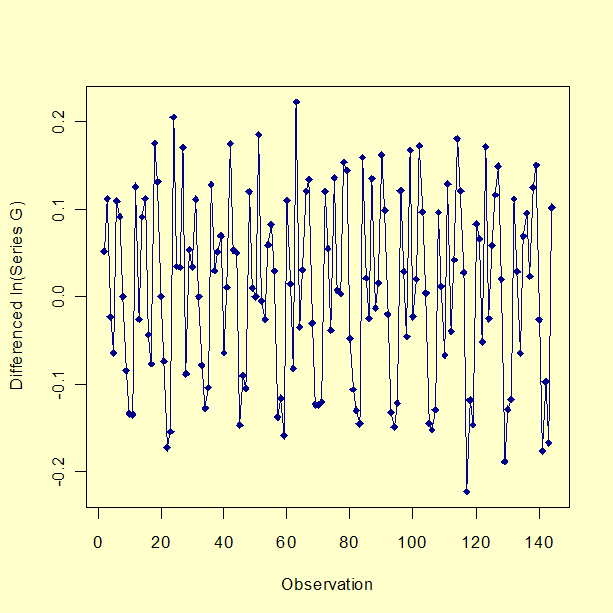
계절성에 대한 자기상관 그래프 분석
적당한 모델을 판별하기 위해, 시계열의 ACF를 그리자.
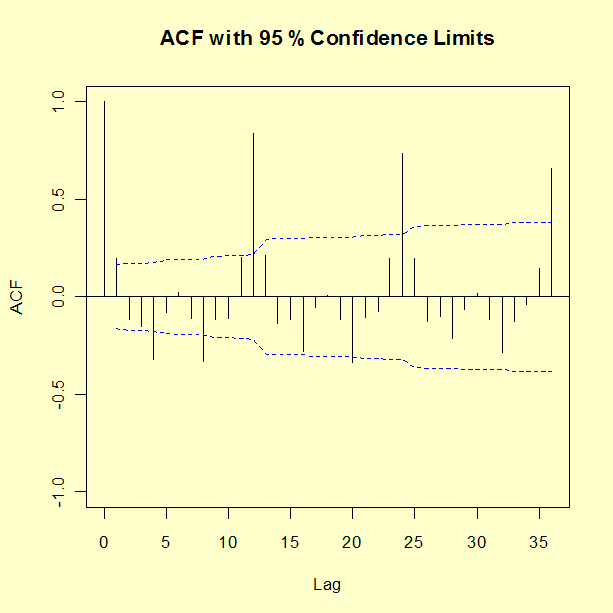
12 뒤처짐이나 24 뒤처짐 같이 \(n\) 주기 떨어져서 아주 큰 자기상관이 보이면, 주기성이 있다고 볼 수 있다. 자기상관을 줄이는 것이 판별 과정의 목적이니 이러한 효과는 제거해야 한다. 그래서 단순하게 차이를 구하는 것으로는 충분하지 않고, 4, 6, 12 같은 특정한 시기에 계절적인 차이를 구해보자. 이 예제에서는 12로 해보자.
다음은 자연 로그를 취하고, 차이를 구하고, 계절적인 차이를 구해서 그린 시계열 G이다.

계절적인 항의 수가 거의 없다. 예측하는 함수의 형태를 안다면, 게절적인 AR 이나 계절적인 MA 모델에 대해 적절한 수의 항을 고를 수 있다.
박스와 젠킨스의 책, 시계열 분석: 예측과 제어 Time Series Analysis Forecasting and Control (the later edition is Box, Jenkins and Reinsel, 1994), 326-328쪽에 관련 내용이 있다. 잘 모르겠지만 차이를 구하기 전에 증가하는 추세는 있다면, 계절적인 MA 항을 골라서 진단 과정에서 어떻게 나오는지 보라.
시계열 G의 자연 로그 차이와 계절적인 차이의 ACF 그래프는 다음과 같다.
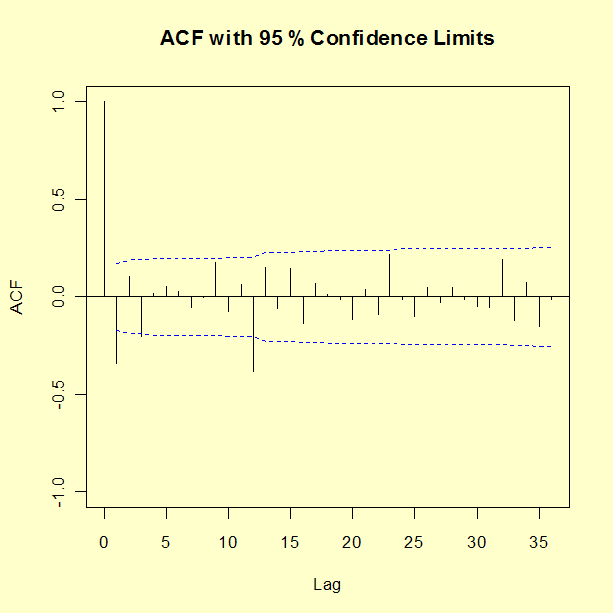
두드러지게 보이는 뾰족한 선 몇 개가 있지만, 자기상관이 거의 0이다. 이 말은, 계절적인 MA(1)가 적합하다는 이야기이다.
| 뒤처짐 | ACF |
|---|---|
| 0 | 1.000000000 |
| 1 | -0.389878319 |
| 2 | 0.304394082 |
| 3 | -0.165554717 |
| 4 | 0.070719321 |
| 5 | -0.097039288 |
| 6 | -0.047057692 |
| 7 | 0.035373112 |
| 8 | -0.043458199 |
| 9 | -0.004796162 |
| 10 | 0.014393137 |
| 11 | 0.109917200 |
| 12 | -0.068778492 |
| 13 | 0.148034489 |
| 14 | 0.035768581 |
| 15 | -0.006677806 |
| 16 | 0.173004275 |
| 17 | -0.111342583 |
| 18 | 0.019970791 |
| 19 | -0.047349722 |
| 20 | 0.016136806 |
| 21 | 0.022279561 |
| 22 | -0.078710582 |
| 23 | -0.009577413 |
| 24 | -0.073114034 |
| 25 | -0.019503289 |
| 26 | 0.041465024 |
| 27 | -0.022134370 |
| 28 | 0.088887299 |
| 29 | 0.016247148 |
| 30 | 0.003946351 |
| 31 | 0.004584069 |
| 32 | -0.024782198 |
| 33 | -0.025905040 |
| 34 | -0.062879966 |
| 35 | 0.026101117 |
모델 맞추기 계절적인 MA(1)을 데이터에 맞춰보자. $$ X_{t} - \delta = A_{t} + \theta_{1} A_{t-1} + \phi_{1} A_{t-12} + \theta_{1} \phi_{1} A_{t-13}, $$ 여기에서 \theta_{1}은 MA(1) 매개변수이고 \phi_{1}은 계절적인 매개변수이다. 모델 맞춘 결과는 다음과 같다.
| 측정 | MA(1) | 계절적인 MA(1) |
|---|---|---|
| 매개변수 | -0.4018 | -0.5569 |
| 매개변수 | 0.0896 | 0.0731 |
나머지 표준 편차 = 0.0367
로그 가능성(Log likelihood) = 244.7
AIC = -483.4
박스-융 테스트로 30 뒤처짐까지 나머지의 무작위성을 확인하였다. 두 측정 매개변수에 대해 기각 영역에 대한 자유도를 맞춰야 한다.
\(H_{0}\) : 나머지가 무작위적이다.
\(H_{a}\) : 나머지가 무작위적이지 않다.
테스트 통계: \( Q = 29.4935 \)
유의미도: \( \alpha = 0.05 \)
자유도: \(h = 30 - 2 = 28\)
기각 값: \( \xi_{1-\alpha, h}^{2} = 41.3371\)
기각 영역: \(Q > 41.3371\) 일 때, \(H_{0}\) 기각
박스-융 테스트의 귀무 가설이 기각되지 않았으니, 맞춘 모델이 적절하다고 볼 수 있다.
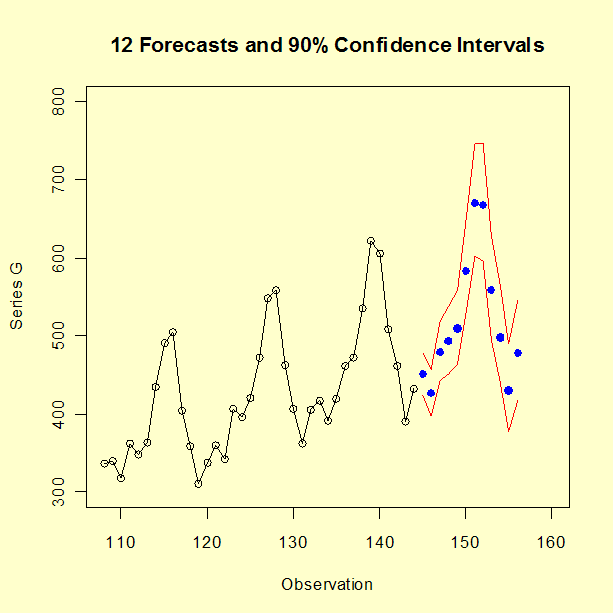
예측 우리의 계절적인 MA(1) 모델로, 12 시점 앞을 예측하고 90% 신뢰 구간도 계산해보자.
| 시점 | 상한값 | 예측 | 상한값 |
|---|---|---|---|
| 145 | 424.0234 | 450.7261 | 478.4649 |
| 146 | 396.7861 | 426.0042 | 456.7577 |
| 147 | 442.5731 | 479.3298 | 518.4399 |
| 148 | 451.3902 | 492.7365 | 537.1454 |
| 149 | 463.3034 | 509.3982 | 559.3245 |
| 150 | 527.3754 | 583.7383 | 645.2544 |
| 151 | 601.9371 | 670.4625 | 745.7830 |
| 152 | 595.7602 | 667.5274 | 746.9323 |
| 153 | 495.7137 | 558.5657 | 628.5389 |
| 154 | 439.1900 | 497.5430 | 562.8899 |
| 155 | 377.7598 | 430.1618 | 489.1730 |
| 156 | 417.3149 | 477.5643 | 545.7760 |