6.4.4.9. 단변량 박스-젠킨스 분석 예제
November 25, 2016
시계열 F Box, Jenkins, and Reinsel, 1994에 있는 시계열 F 데이터를 살펴보자. 다음 그래프에서 볼 수 있는 것처럼 원본 데이터에는 70개의 점이 있다.
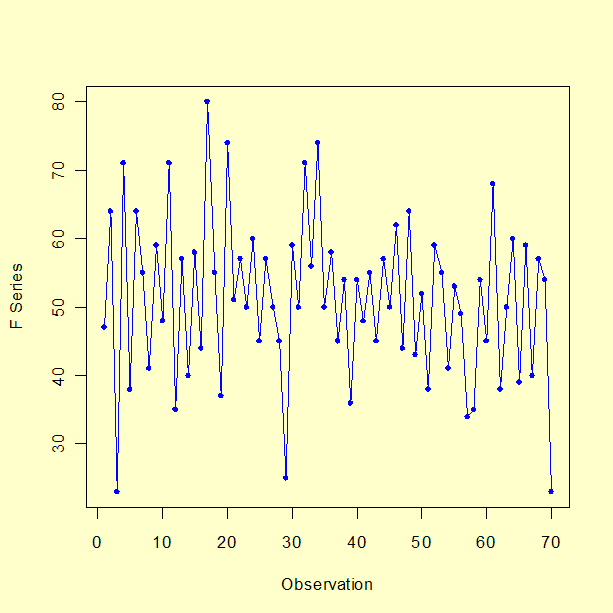
데이터에 계절적인 성분이나 눈에 띄는 추세가 있는 것 같진 않다. (직선을 데이터에 맞춰 시계열의 정상성을 확인했다. 0에서 많이 차이나는 기울기가 보이진 않았다. p-값 = 0.2)
6.4.4.10절에서 나머지 시계열에 박스-융 테스트를 다루는 예제가 있다.
모델 판별 데이터를 맞추기 위한 모델의 종류를 정하기 위해 첫 35 뒤처짐에 대한 데이터의 자기상관 함수(ACF)를 보자. 결과와 ACF를 95% 신뢰 구간과 함께 뒤처짐에 따라 그려보자.
| 뒤처짐 | ACF |
|---|---|
| 0 | 1.000000000 |
| 1 | -0.389878319 |
| 2 | 0.304394082 |
| 3 | -0.165554717 |
| 4 | 0.070719321 |
| 5 | -0.097039288 |
| 6 | -0.047057692 |
| 7 | 0.035373112 |
| 8 | -0.043458199 |
| 9 | -0.004796162 |
| 10 | 0.014393137 |
| 11 | 0.109917200 |
| 12 | -0.068778492 |
| 13 | 0.148034489 |
| 14 | 0.035768581 |
| 15 | -0.006677806 |
| 16 | 0.173004275 |
| 17 | -0.111342583 |
| 18 | 0.019970791 |
| 19 | -0.047349722 |
| 20 | 0.016136806 |
| 21 | 0.022279561 |
| 22 | -0.078710582 |
| 23 | -0.009577413 |
| 24 | -0.073114034 |
| 25 | -0.019503289 |
| 26 | 0.041465024 |
| 27 | -0.022134370 |
| 28 | 0.088887299 |
| 29 | 0.016247148 |
| 30 | 0.003946351 |
| 31 | 0.004584069 |
| 32 | -0.024782198 |
| 33 | -0.025905040 |
| 34 | -0.062879966 |
| 35 | 0.026101117 |
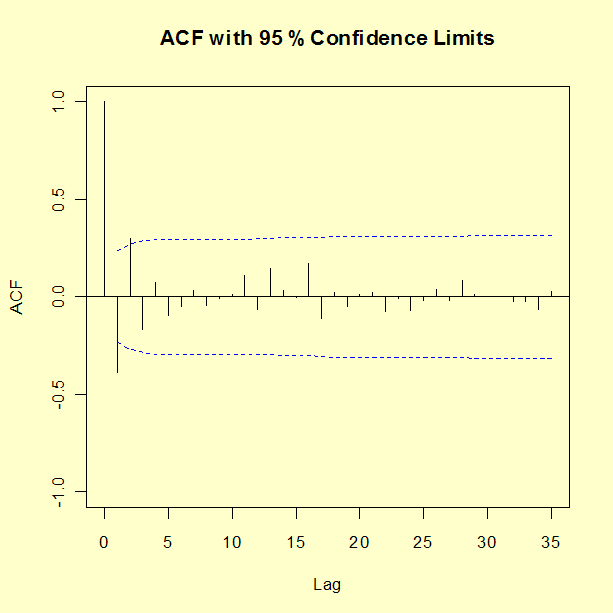
ACF 값의 부호가 왔다갔다하다가 2 뒤처짐 이후로 빠르게 감소한다. 이것은 AR(2) 모델이 데이터에 적합하다는 의미이다.
모델 맞추기 AR(2) 모델을 데이터에 맞추자. $$ X_{t} = \delta + \phi_{1} X_{t-1} + \phi_{2} X_{t-2} + A_{t} $$
아래는 모델을 맞춘 결과이다.
| 소스 | 측정 | 표준 오차 |
|---|---|---|
| \( \phi_{1} \) | -0.3198 | 0.1202 |
| \( \phi_{2} \) | 0.1797 | 0.1202 |
\( \delta = 51.1286 \)
나머지 표준 편차 = 10.9599
나머지의 테스트 무작위성:
표준화된 통계
Z = 0.4887, p-값 = 0.625
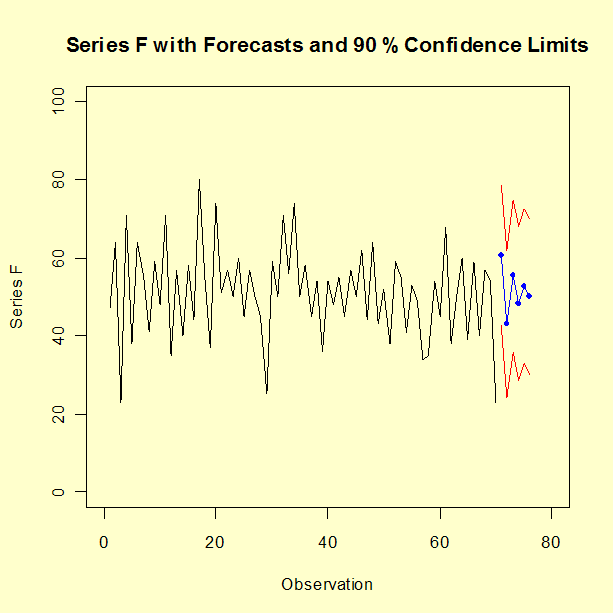
예측 지금까지 다룬 AR(2) 모델로 6 시점 앞까지 예측해보자.
| 시점 | 예측 | 표준 오차 |
|---|---|---|
| 71 | 60.6405 | 10.9479 |
| 72 | 43.0317 | 11.4941 |
| 73 | 55.4274 | 11.9015 |
| 74 | 48.2987 | 12.0108 |
| 75 | 52.8061 | 12.0585 |
| 76 | 50.0835 | 12.0751 |
이전 데이터와 예측한 값을 (90% 신뢰 구간과 함께) 그리면 다음과 같다.