6.4.4.3. 계절성(Seasonality)
November 23, 2016
계절성 많은 시계열은 계절성을 나타낸다. 계절성은 주기적인 변동을 의미한다. 예를 들면, 소매 형태 판매량의 시계열은 크리스마스 기간에 최고조에 다다르고 나서 기간이 지나면 감소한다. 그래서 소매 형태 판매량의 시계열은 보통 9월부터 12월까지 증가하는 추세를, 1월과 2월에 감소하는 추세를 보인다.
경제 분야 시계열에서 계절성은 아주 흔한 현상이지만, 공학이나 과학 분야 시계열에서는 그렇지 않다.
계절성이 나타나면, 시계열 모델에서 반드시 고려해야 한다. 이 절에서는 계절성을 감지하는 기법을 살펴보자. 계절성을 모델링하는 작업은 이후의 절에서 다루겠다.
계절성을 감지하기 계절성을 감지하기 위해 다음의 기법을 사용할 수 있다.
1. 진행 순서 그래프가 종종 계절성을 보여준다.
2. 계절적인 부 시계열(subseries) 그래프는 계절성을 보여주기 위한 전문적인 기법이다.
3. 다중 상자 그래프(multiple box plots)도 계절적인 부 시계열 그래프에서 계절성을 감지하기 위해 사용할 수 있다.
4. 자기상관 그래프는 계절성을 확인하는데 도움이 된다.
아래는 각 그래프에 해당하는 예제이다.
어떤 시계열을 분석할 때 첫 단계에서 진행 순서 그래프를 사용하길 추천한다. 가끔 이 그래프에서 계절성이 나타나더라도, 계절적인 부 시계열이나 상자 그래프로 더욱 분명하게 확인할 수 있다. 계절적인 부 시계열 그래프는 계절적인 차이와 그룹 내부 패턴 모두를 확인하는데 매우 좋다. 상자 그래프는 (그룹 패턴들 사이의) 계절적인 차이를 꽤 잘 보여주지만, 그룹 내부의 패턴을 보여주지는 않는다. 하지만, 큰 데이터가 있을 때, 보통 상자 그래프가 계절적인 부 시계열 그래프보다 읽기 쉽다.
계절적인 부 시계열 그래프와 상자 그래프 모두 계절 주기를 알고 있다고 가정한다. 사실 대부분의 경우에, 분석하는 사람은 이것을 알게 된다. 예를 들면, 월별 데이터에서 1년에 12달이 있으니 주기는 12이다. 하지만 주기를 모르면, 자기 상관 그래프를 사용하자. 의미있는 계절성이 있으면, 자기 상관 그래프에서 주기와 같은 어떤 뒤처짐 값에서 뾰족한 막대 모양이 나타난다. 예를 들면, 월별 데이터에 계절성 효과가 있으면, 12, 24, 36 등의 뒤처짐 값에서 (뒤처짐 값이 커질 수록 막대 그래프 크기가 줄어들긴 하지만) 의미있는 막대 그래프가 나타날 것이다.
계절성이 없는 예제 다음은 엘니뇨를 예측하기 위한 남방 진동 데이터를 나타내는 그래프이다.
진행 순서 그래프
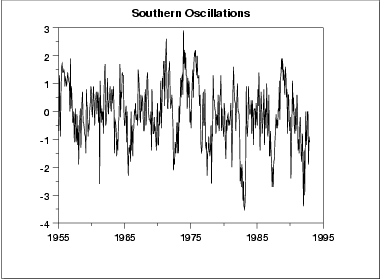
진행 순서 그래프에서 분명하게 나타나는 주기적 패턴이 없다.
계절적인 부 시계열 그래프
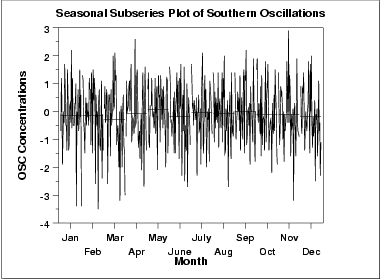
각 월의 평균값이 거의 비슷하다. 분명하게 나타나는 패턴이 없다.
상자 그래프
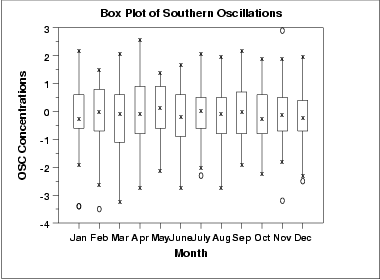
계절적인 부 시계열 그래프처럼, 분명하게 나타나는 패턴이 없다.
관측값이 상당히 많아서 상자 그래프가 계절적인 부 시계열 그래프보다 월별 차이를 더 잘 보여준다.
계절성이 있는 예제
다음은 월별 이산화탄소 농도 데이터를 나타내는 그래프이다. 선형 추세는 제거한 것이다.
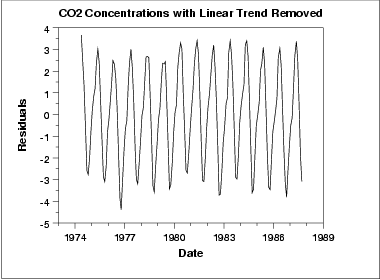
이 그래프는 주기적인 성질을 나타낸다. 하지만, 이 그래프에서 계절성이 있다고 판단하기는 힘들다.
상자 그래프
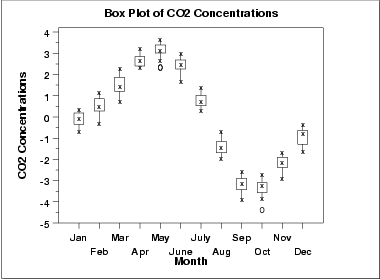
계절적인 부 시계열 그래프처럼, 상자 그래프에서도 계절적인 패턴이 상당히 분명하게 나타난다.