6.4.4.2. 정상성(Stationarity)
November 23, 2016
정상성 흔히 많은 시계열 기법들은 데이터가 정상적(stationary)이라고 가정한다.
정상 과정(stationary process)은 평균, 분산, 자기상관 구조가 시간에 따라서 변하지 않는 특징이 있다. 정상성은 정확한 수학적 용어로 정의할 수 있지만, 이 글에서는 추세를 무시하면, 분산이 일정하고, 시간에 따라 일정한 자기상관 구조가 있으며, 주기적인 변동(계절성)이 없는 평평한 시계열 정도로 이야기하면 충분하다.
실용적인 목적에서 보통 진행 순서 그래프(run sequence plot)를 보고 정상성을 판단할 수 있다.
정상성을 다루기 위한 변환 시계열이 정상(stationary)적이지 않으면, 다음과 같은 기법으로 시계열을 변환해서 종종 정상성을 확인할 수 있다.
1. 주어진 시계열 Z_{t}에서 다음과 같이 차이를 구하여 새로운 시계열을 만든다. $$ Y_{i} = Z_{i} - Z_{i-1} $$ 차이로 구한 데이터는 원본 데이터보다 한 점이 적다. 한 번 이상 차이를 구할 수 있긴 하지만, 보통 한 번만 구해도 충분하다.
2. 데이터에 추세가 있다면, 데이터를 어떤 종류의 곡선으로 맞추고 데이터와 곡선과의 차이를 모델링한다. 단순히 장기적인 추세를 없애려고 곡선으로 맞추기 때문에 보통 직선으로 단순하게 맞춘다.
3. 일정하지 않은 분산이 있는 경우는, 시계열에 로그나 제곱근을 취하여 분산을 안정시킨다. 데이터에 음수가 있는 경우는 모든 데이터 값을 상수로 만드는 적절한 상수를 더한다. 이 상수는 미래 예측값을 구할 때 다시 빼면 된다.
일정한 위치와 척도를 나타내는 시계열을 만들기 위해 위의 기법을 소개하였다. 계절성에 정상성이 없더라도, 보통 시계열 모델에 포함되어있다.
예제 다음은 월별 이산화탄소 농도 데이터 그래프이다.
진행 순서 그래프
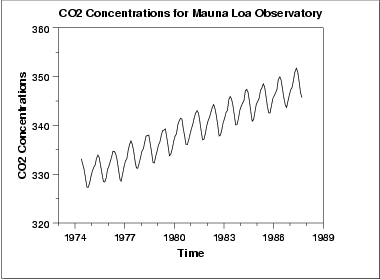
데이터의 진행 순서 그래프가 증가 추세를 나타낸다. 육안으로 이 그래프를 보면 증가 추세를 없애려면 단순하게 직선 함수로 맞춰도 충분하다는 것을 알 수 있다.
이 그래프에서 주기적인 성질도 볼 수 있다. 이 부분은 다음 절에서 다룰 것이다.
선형 추세 제거
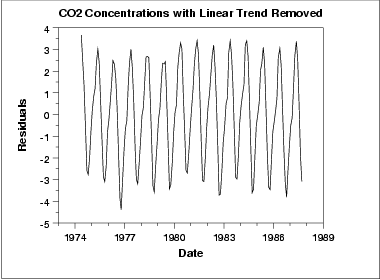
데이터의 진행 순서 그래프가 증가 추세를 나타낸다. 육안으로 이 그래프를 보면 증가 추세를 없애려면 단순하게 직선 함수로 맞춰도 충분하다는 것을 알 수 있다.