6.4.3.1. 단일 지수 평활법
November 19, 2016
지수 평활법은 미래 값을 예측하기 위해 과거 관측값을 지수적으로 감소하는 가중치로 다룬다 이 평활법은 \( S_{2} \) 를 \( y_{1} \)로 두는 것부터 시작한다. \( S_{i} \)는 평활화한 관측이나 EWMA (Exponentially Weighted Moving Average)를, \( y \)는 원래의 관측값을 나타낸다. 아래 첨자는 시기를 의미한다\( (1, 2, ..., n) \). 3번째 시기에 대해 다음과 같이 쓸 수 있다. \( S_{3} = \alpha y_{2} + (1-\alpha)S_{2} \). 다른 시기에 대해서도 마찬가지로 쓸 수 있지만, \( S_{1} \) 값은 없다.
어떤 시기 \( t \)에 대해, 평활화한 값 \( S_{i} \) 는 다음과 같이 계산할 수 있다. $$ S_t = \alpha y_{t-1} + (1-\alpha)S_{t-1} \qquad 0 < \alpha \le 1 \qquad t \ge 3 $$
이것이 지수 평활법의 기본 등식이고, 상수 또는 매개변수 \( \alpha \) 를 평활 상수라고 한다.
메모: 기본 등식에서 \( y_{t-1} \)을 \( y_{t} \)로 바꾼 방법도 있다. EWMA 제어 차트 절에 Robert가 1959년에 제안한 이 방법을 서술하였다. 여기에서 사용하는 등식은 1986년에 Hunter가 제안한 것을 따른다.
첫 번째 EWMA 설정하기
첫 번째 예측이 아주 중요하다 첫 번째 EWMA는 다음에 나오는 모든 EWMA 값을 계산하는데 중요한 역할을 한다. \( S_{2} \)를 \( y_{1} \)로 정하는 것은 일종의 초기화이다. 다른 방법으로 정할 수도 있다.
처음 4개나 5개의 관측값을 평균할 것인지도 정할 수 있다.
\( \alpha \) 값이 작을 수록 첫 번째 EWMA를 정하는 것이 중요하게 된다. 초기 설정을 확정하기 전에 몇 가지 방법들을 시도해보길 바란다(여기에서는 사용하는 소프트웨어가 이러한 기능을 지원하고 있다는 것을 가정하고 있다).
왜 "지수"라는 말이 들어가는가?
기본 등식을 전개하기 먼저 S_{t-1}를 기본 등식에 대입해서 전개하면 다음과 같은 식을 얻을 수 있다. $$ \begin{align*} S_{t} & = \alpha y_{t-1} + (1-\alpha)\left[ \alpha y_{t-2} + (1-\alpha)S_{t-2} \right] \\ & = \alpha y_{t-1} + \alpha(1-\alpha) y_{t-2} + (1-\alpha)^{2}S_{t-2} \end{align*} $$
기본 등식에 관한 합 공식 \( S_{2} \)가 나올 때까지 \( S_{t-2}, S_{t-3}, \cdots \) 이런 식으로 대입하면 다음과 같은 전개식을 쓸 수 있다. $$ S_{t} = \alpha \sum_{i=1}^{t-2} (1-\alpha)^{i-1} y_{t-i} + (1-\alpha)^{t-2} S_{2} \ , \qquad t \ge 2 $$
\( S_5 \)에 대하여 전개한 등식 예를 들면, \( S_5 \)에 대해 전개한 식은 다음과 같다. $$ S_{5} = \alpha \left[ (1-\alpha)^{0} y_{5-1} + (1-\alpha)^{1} y_{5-2} + (1-\alpha)^{2} y_{5-3} \right] + (1-\alpha)^{3} S_{2} $$
지수적인 성질을 보인다 이 식은 지수적인 성질을 보인다. 가중치 \( \alpha(1-\alpha)^{t} \) 는 기하적으로 감수하며, 기하 급수의 성질을 이용하면 다음과 같이 합은 1이다. $$ \alpha \sum_{i=0}^{t-1} (1-\alpha)^{i} = \alpha \left[ \frac{ 1 - (1-\alpha)^{t} }{ 1 - (1-\alpha) } \right] = 1 - (1-\alpha)^{t} $$ 위의 식에서 보면, \( t \)가 증가할 수록 평활화한 \( S_t \)의 영향이 점점 작아지는 것을 알 수 있다.
\( \alpha=0.3 \) 일 때 예제 \( \alpha=0.3 \)인 경우, 가중치 \( \alpha(1-\alpha)^{t} \)는 시간에 따라 지수적으로(기하적으로) 감소한다.
| 값 | 가중치 |
|---|---|
| \( y_{1} \) | 0.2100 |
| \( y_{2} \) | 0.1470 |
| \( y_{3} \) | 0.1029 |
| \( y_{4} \) | 0.0720 |
어떤 \( \alpha \)가 "가장" 좋은 값인가?
가중치 매개변수를 어떻게 선택할 것인가? 오래된 값을 평활화하는 빠르기는 \( \alpha \)값의 함수이다. \( \alpha \)가 1에 가까우면 빠르게 평활화가 일어나고, 0에 가까우면 느리게 일어난다. 다음의 표는 이와 같은 과정을 보여준다.
과거의 관측값 방향 → → → → → → →
| \( \alpha \) | \( (1-\alpha) \) | \( (1-\alpha)^{2} \) | \( (1-\alpha)^{3} \) | \( (1-\alpha)^{4} \) |
|---|---|---|---|---|
| 0.9 | 0.1 | 0.01 | 0.001 | 0.0001 |
| 0.5 | 0.5 | 0.25 | 0.125 | 0.0625 |
| 0.1 | 0.9 | 0.81 | 0.729 | 0.6561 |
가장 작은 MSE를 얻을 수 있는 \( \alpha \) 값이 가장 좋은 값이다.
예제 지금까지의 배운 내용을 가지고 예제 하나를 다뤄보자. 다음과 같이 시간에 따라 수집한 12개의 관측값이 있는 상황을 생각해보자.
| 시점 | \( y_{t} \) | \( S(\alpha=0.1) \) | 오차 | 제곱 오차 |
|---|---|---|---|---|
| 1 | 71 | |||
| 2 | 70 | 71 | -1.00 | 1.00 |
| 3 | 69 | 70.9 | -1.90 | 3.61 |
| 4 | 68 | 70.71 | -2.71 | 7.34 |
| 5 | 64 | 70.44 | -6.44 | 41.47 |
| 6 | 65 | 69.80 | -4.80 | 23.04 |
| 7 | 72 | 69.32 | 2.68 | 7.18 |
| 8 | 78 | 69.58 | 8.42 | 70.90 |
| 9 | 75 | 70.43 | 4.57 | 20.88 |
| 10 | 75 | 70.88 | 4.12 | 16.97 |
| 11 | 75 | 71.29 | 3.71 | 13.76 |
| 12 | 70 | 71.67 | -1.67 | 2.79 |
제곱 오차의 합(SSE)은 208.94이고, 제곱 오차의 평균(MSE)은 SSE / 11 = 19.0 이다.
다른 \( \alpha \) 값에 대해 계산하기 \( \alpha=0.5 \) 인 경우에 MSE를 계산하면 16.29를 얻을 수 있다. 더 좋은 값을 얻을 수 있을까? 시행착오(trial-and-error) 접근법을 적용해볼 수 있다. \( \alpha \)를 0.1부터 0.9까지 탐색하고 그 중에서 가장 좋은 \( \alpha \)를 선택한 다음, \( \alpha-\Delta \)와 \( \alpha+\Delta \) 범위에서 작업을 반복한다. 한 번 더 반복하면, 소수점 3째 자리 정확도를 가지는 \( \alpha \)를 찾을 수 있다.
비선형 최적화를 사용할 수 있다 하지만 마르쿼트(Marquardt) 방법 같은 더 좋은 탐색법이 있다. 이 방법은 실제 값과 추정 값의 차이(residual) 제곱 합을 최소화하는 비선형 최적화 기법이다. 일반적으로 보통 좋은 통계 프로그램들은 MSE를 최소화하는 \( \alpha\)를 찾아준다.
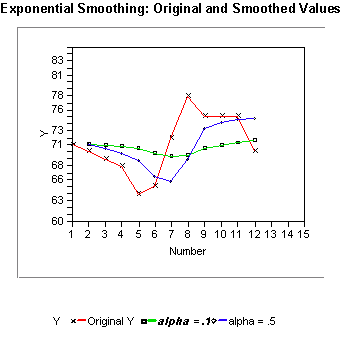
2개의 \( \alpha \) 에 대해 평활화한 데이터를 보여주는 그래프