6.4.4.6.3. 부분 자기상관 그래프
November 25, 2016
목적: 박스-젠킨스 모델 판별 부분 자기상관 그래프(Box and Jenkins, pp. 64-65, 1970)는 박스-젠킨스 모델 판별 과정에서 흔히 사용하는 방법이다.
\(k\) 뒤처짐에서 부분 상관은 \(1\) 뒤처짐 부터 \(k-1\) 뒤처짐으로 설명하지 않은 \( X_{t} \)와 \( X_{t-k} \) 사이의 자기상관이다.
여기에서 소개하지 않았지만 표본 자기상관에 기초를 두고 부분 자기 상관을 계산하는 다른 알고리즘도 있다. 자세한 내용은 Box, Jenkins, and Reinsel 1970 이나 Brockwell, 1991을 보라.
특별히, 부분 자기상관은 자동회귀 모델의 차수를 판별할 때 사용하면 좋다. \( AR(p) \) 과정의 부분 상관은 \(p+1\) 이상의 뒤처짐에서 0이다. 표본 자기상관 그래프가 어떤 AR 모델이 적합할 수도 있다는 것을 보여주면, 차수를 판별하기 위해 표본 부분 자기상관 그래프를 확인하자. 부분 자기상관이 0이 되기 시작하는 점을 보자. 이 때 통계적 유의미함에 대한 95% 신뢰 구간을 사용하면 좋다.
근사적으로 부분 자기상관에 대한 95% 신뢰 구간은 \( \pm 2 / \sqrt{N} \) 이다.
표본 그래프
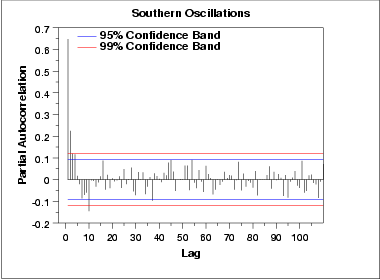
이 부분 자기상관 그래프에서 \(1\) 뒤처짐과 \(2\) 뒤처짐(\(0\) 뒤처짐의 \(y\)값은 항상 \(1\)이다)에 대해 분명한 통계적인 유의미함을 볼 수 있다. 이후의 몇몇 뒤처짐은 경계선에 걸친다. 자기상관 그래프에서 AR 모델이 적합하다고 알 수 있으면, \( AR(2) \) 모델로 모델링을 시작할 수 있을 것이다. 이것을 \( AR(3) \)과 비교해보겠다.
정의 부분 자기상관 그래프의 구성 요소이다.
수직 축: h 뒤처짐에서 부분 자기상관 계수
수평 축: 시간 뒤처짐 h (h=0,1,2,3, ...).
그리고 여기에 95% 신뢰 구간을 그린다.
질문 부분 자기상관 그래프로 다음과 같은 질문에 답할 수 있다.
1. AR 모델이 데이터에 적합한가?
2. AR 모델이 적합하다면, 차수는 얼마인가?
관련 기법
자기상관 그래프
연속순서 그래프
분광 그래프
사례 연구 Negiz 데이터 사례 연구에 부분 자기상관 그래프가 있다.
소프트웨어 많은 통계 소프트웨어에서 부분 자기상관 그래프를 지원한다.