6.4.4.6.2. 이산화탄소 농도 데이터에서 모델 판별

November 25, 2016

⊕ 월별 이산화탄소 농도 에제 두 번째 예제는 월별 이산화탄소 농도 데이터이다. 첫 번째 예제처럼, 먼저 정상성을 확인하기 위해 진행 순서 그래프(Run sequence plot)를 보자.

⊕ 진행 순서 그래프

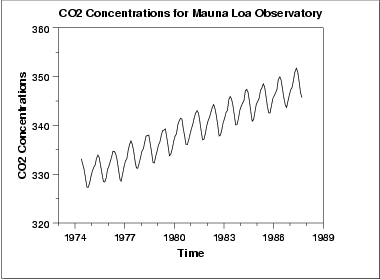
데이터의 진행 순서 그래프에서 증가 추세가 보인다. 단순한 직선으로 증가 추세를 충분히 맞출 수 있을 것 같다.

⊕ 계절적인 부 시계열 그래프

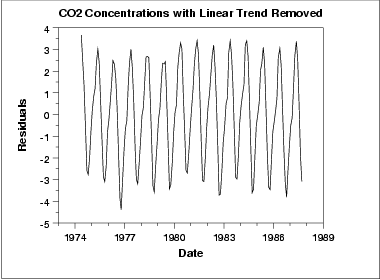
여기에서 \(y\)축은 원 데이터에서 맞춘 직선을 뺀 나머지이다. 선형 추세를 제거하고나니, 진행 순서 그래프는 일정한 위치에 놓였고 일정한 분산을 가지는 것을 볼 수 있다. 이러한 경향은 정상성(stationarity)을 의미한다.

하지만, 그래프에 게절성(seasonality)이 없다. 주기를 정하기 위해 자기상관함수를 확인하고 주기적 부 시계열 그래프를 살펴보자.

⊕ 자기상관 그래프

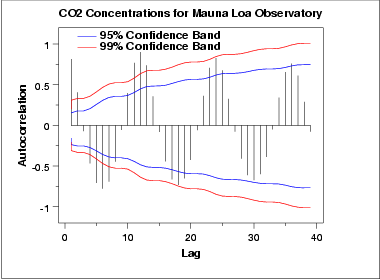
자기상관 그래프에서 뾰족한 양수와 음수 막대가 반복하여 나타난다. 12 뒤처짐마다 패턴이 반복되는 것도 보인다. 이것은 계절성 효과와 관련 있다.

자기상관 그래프에서 두 선은 자기상관의 통계적인 유의미함에 대한 95%와 99% 신뢰 구간이다.

⊕ 계절적인 부 시계열 그래프

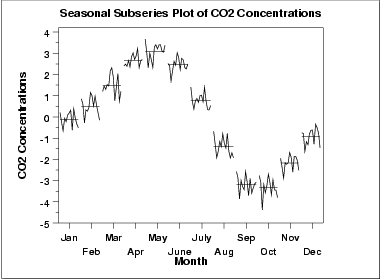
그래프에서 의미있는 계절적인 패턴이 분명하게 보이니, 박스-젠킨스 모델을 맞출 때 계절적인 항을 추가해야 한다. 월별 데이터라서 12 뒤처짐 계절적인 자동회귀나(와) 이동 평균 항을 추가하자.

비-계절적 성분을 잘 판별하기 위해 12라는 계절적인 차이를 고려하고 계절적인 차이를 고려한 데이터에서 자기상관 그래프를 보자.

⊕ 계절적인 차이를 고려한 데이터의 자기상관 그래프

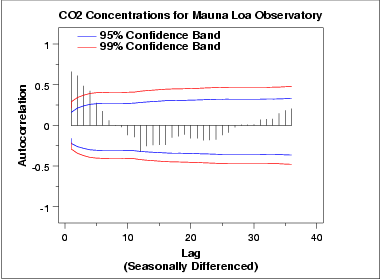
위의 자기상관 그래프에 지수적인 감소와 감쇠 사인 패턴이 혼합된 형태가 보인다. 차수가 1보다 큰 AR 모델이 적절한 것 같다. 차수를 잘 판별하기 위해 부분 자기상관 그래프를 보자.

⊕ 계절적인 차이를 고려한 데이터의 자기상관 그래프

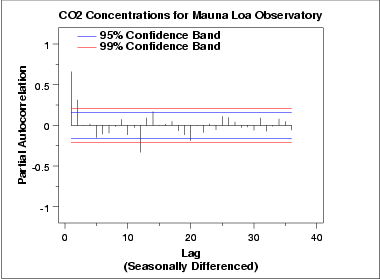
부분 자기상관 그래프에서 부분 자기상관이 두 번째 뒤처짐부터 0이 되는 것을 보니 AR(2) 모델이 적합한 것 같다. 어떤 종류의 나머지 계절성을 의미하는 뒤처짐 12도 두드러지게 보인다.

요약하면, 선형 추세를 제거한 데이터에 대한 계절적인 AR(12) 항이 있는 AR(2) 모델이 적합했다. 계절적인 차이를 적용했을 때와 그렇지 않았을 때도 할 수 있을 것이다. 모델을 결정하기 전에 꼭 모델을 검증해야 한다.