6.4.3.4. 이중 지수 평활법을 이용한 예측(LASP)
November 19, 2016
예측 식 한 시점 앞을 예측하는 식은 다음과 같이 쓸 수 있다. $$ F_{t+1} = S_{t} + b_{t} $$ m 시점 앞을 예측하는 식은 다음과 같이 쓸 수 있다. $$ F_{t+m} = S_{t} + m b_{t} $$
예제 다음의 데이터를 다시 한 번 살펴보자.
6.4, 5.6, 7.8, 8.8, 11, 11.6, 16.7, 15.3, 21.6, 22.4.
\( \alpha=0.3623 \)과 \( \gamma=1.0 \)인 이중 평활법 모델로 맞춰보자. 이 두 매개변수는 원본 시게열을 한 시점 앞 예측과 비교하여 최소 MSE값과 가까운 것이다(지금 다루는 이중 지수 평활법은 평활값을 계산하기 위해 현재 시계열 값을 사용한다). 초기값은 다음과 같다. $$ \begin{align*} S_{1} &= y_{1} = 6.4 \\ b_{1} &= \frac{1}{3} \left[ (y_{2} - y_{1}) + (y_{3} - y_{2}) + (y_{4} - y_{3}) \right] \end{align*} $$ 대조군으로 \( \alpha=0.977\)일 때의 단일 평활 모델도 해보자. 이 \( \alpha \) 값은 단일 지수 평활법에서 최소 MSE와 가까운 값이다.
예제 결과 예측 예제에서 평활 결과는 다음과 같다.
| 데이터 | 이중 | 단일 |
|---|---|---|
| 6.4 | 6.4 | |
| 5.6 | 6.6 (예측 = 7.2) | 6.4 |
| 7.8 | 7.2 (예측 = 6.8) | 5.6 |
| 8.8 | 8.1 (예측 = 7.8) | 7.8 |
| 11.0 | 9.8 (예측 = 9.1) | 8.8 |
| 11.6 | 11.5 (예측 = 11.4) | 10.9 |
| 16.7 | 14.5 (예측 = 13.2) | 11.6 |
| 15.3 | 16.7 (예측 = 17.4) | 16.6 |
| 21.6 | 19.9 (예측 = 18.9) | 15.3 |
| 22.4 | 22.8 (예측 = 23.1) | 21.5 |
예측값 비교
표는 단일 및 이중 지수 평활법으로 예측한 결과를 나타낸다 각 방법이 미래를 어떻게 예측했는지 살펴보기 위해, 가장 마지막 관측값 이후 5개 시점을 계산하면,
| 시점 | 단일 | 이중 |
|---|---|---|
| 11 | 22.4 | 25.8 |
| 12 | 22.4 | 28.7 |
| 13 | 22.4 | 31.7 |
| 14 | 22.4 | 34.6 |
| 15 | 22.4 | 37.6 |
단일 및 이중 지수 평활법으로 예측한 결과를 비교하는 그래프 결과를 나타내는 그래프로 보면 아주 명확하게 차이를 볼 수 있다.
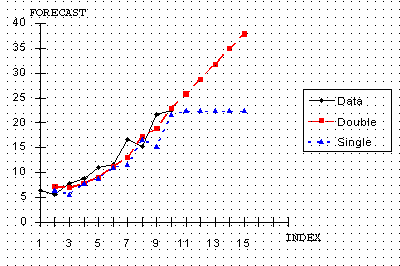
이 그래프에서 보니 이중 평활법 경우가 단일 평활법보다 데이터에 훨씬 더 가깝다. 단일 평활법은 예측할 때 단순하게 수평선과 다를바가 없다는 것도 알 수 있다. 실제 상황에서 이런 수평선과 같은 상황이 일어날 가능성은 낮다. 따라서 이 경우에는 이중 평활법이 낫다.
이중 지수 평활법과 회귀법으로 예측한 결과를 비교하는 그래프 선형 회귀법과 이중 지수 평활법을 비교해보자.
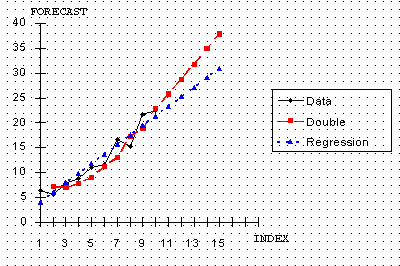
꽤 재미있는 그림이다. 두 기법 모두 비슷한 경향을 따르지만, 회귀선은 이중 평활법에 비해 예측값이 느리게 증가한다.
예측하는 사람마다 다른 기법을 선택한다 예측하는 사람에 따라 선택하는 기법이 다르다. 성장과정을 공격적으로 나타내고 싶으면, 이중 평활법을 선택한다. 아니면, 회귀법을 사용할 것이다. 선형 회귀법에서 "시간"은 독립 변수 역할을 한다. 4장에서 선형 회귀의 기본적인 내용과 회귀 추정의 세부 사항을 이야기했다.