6.4.2. 이동 평균과 평활법이란?
November 19, 2016
데이터 평활은 무작위적인 변화를 줄이고 추세와 주기적인 요소를 보여준다 시간에 따라 수집한 데이터에는 무작위적인 변화량이 있다. 무작위적인 변화로 생기는 효과를 줄이기 위한 방법들이 있다. 산업에서 흔히 사용하는 기법은 "평활"이다. 이 방법을 제대로 사용하면 추세, 계절성, 주기성과 관련된 구성 요소를 더욱 분명하게 확인할 수 있다.
두 가지 평활법이 있다.
- 평균법
- 지수 평활법
평균을 계산하는 것은 가장 단순한 평활법이다 먼저, 모든 과거 데이터의 단순 평균을 계산하는 방법 같은 몇 가지 평균법을 살펴보자.
어떤 창고를 운영하는 사람이 공급자가 얼마나 많이 배달하는지 1000 달러 단위로 알고 싶어하는 경우를 생각해보자. 운영자는 무작위로 12명을 선택하여 다음과 같은 결과를 얻었다.
| 공급자 | 공급량 |
|---|---|
| 1 | 9 |
| 2 | 8 |
| 3 | 9 |
| 4 | 12 |
| 5 | 9 |
| 6 | 12 |
| 7 | 11 |
| 8 | 7 |
| 9 | 13 |
| 10 | 9 |
| 11 | 11 |
| 12 | 10 |
위에서 공급량의 평균값은 10이다. 운영자는 이 값을 표본을 대표하는 공급자의 비용으로 사용하기로 결정했다.
과연 잘 추정한 것일까?
위의 예제에서 MSE 결과 결과는 다음과 같다.
오차와 제곱 오차의 경우
추정치 = 10
| 공급자 | $ | 오차 | 제곱오차 |
|---|---|---|---|
| 1 | 9 | -1 | 1 |
| 2 | 8 | -2 | 4 |
| 3 | 9 | -1 | 1 |
| 4 | 12 | 2 | 4 |
| 5 | 9 | -1 | 1 |
| 6 | 12 | 2 | 4 |
| 7 | 11 | 1 | 1 |
| 8 | 7 | -3 | 9 |
| 9 | 13 | 3 | 9 |
| 10 | 9 | -1 | 1 |
| 11 | 11 | 1 | 1 |
| 12 | 10 | 0 | 0 |
SSE = 36 그리고 MSE = 36/12 = 3
다른 추정값을 사용한 MSE 결과표 각 공급자에 대한 소비량 추정치가 얼마나 좋은가? 10을 7, 9, 12와 비교해보자.
| 지표 | 7 | 9 | 10 | 12 |
|---|---|---|---|---|
| SSE | 144 | 48 | 36 | 84 |
| MSE | 12 | 4 | 3 | 7 |
가장 작은 MSE를 보이는 추정치가 가장 좋은 것이다. 위의 표에서 평균으로 구한 MSE가 가장 작다는 것을 수학적으로 알 수 있다.
표본 데이터의 평균에 대한 제곱 오차를 보여주는 표 평균이 시간에 따른 순이익을 얼마나 잘 예측하는지 살펴보자.
다음은 1985년부터 1994년까지 어떤 컴퓨터 제조사의 세금 공제전 수입을 나타내는 표이다.
| 연도 | $ (백만) | 평균 | 오차 | 제곱 오차 |
|---|---|---|---|---|
| 1985 | 46.163 | 48.676 | -2.513 | 6.313 |
| 1986 | 46.998 | 48.676 | -1.678 | 2.814 |
| 1987 | 47.816 | 48.676 | -0.860 | 0.739 |
| 1988 | 48.311 | 48.676 | -0.365 | 0.133 |
| 1989 | 48.758 | 48.676 | 0.082 | 0.007 |
| 1990 | 49.164 | 48.676 | 0.488 | 0.239 |
| 1991 | 49.548 | 48.676 | 0.872 | 0.761 |
| 1992 | 48.915 | 48.676 | 0.239 | 0.057 |
| 1993 | 50.315 | 48.676 | 1.639 | 2.688 |
| 1994 | 50.768 | 48.676 | 2.092 | 4.378 |
MSE = 1.8129
추세가 있을 때 평균은 좋은 지표가 아니다 추세가 있을 것 같을 때, 수입을 예측할 때 평균을 사용할 수 있을까? 아래의 그래프에서 보면, 사용하면 안 된다는 것을 알 수 있다.
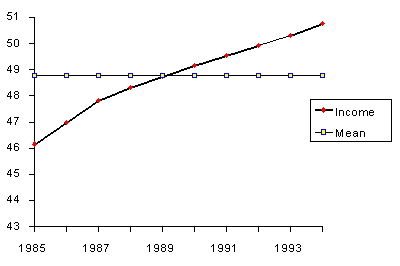 가로축은 연도, 세로축은 수입
가로축은 연도, 세로축은 수입
평균은 모든 과거 관측값을 동일한 가중치로 다룬다 요약하면,
- 1. 단순 평균이나 모든 과거 관측값의 평균은 추세가 없을 때만 쓸모 있다. 추세가 있으면, 추세를 고려하는 다른 측정량을 사용하자.
- 2. 평균은 모든 과거 관측값을 동일하게 다룬다. 예를 들면, 3, 4, 5의 평균값은 4이다. 물론, 우리는 모든 값을 더해서 값의 갯수로 나눠서 평균을 구한다는 것을 알고 있다. 아래와 같이 각 값을 값의 갯수로 나눈 값을 더해서 평균을 구할 수도 있다. $$ 3/3 + 4/3 + 5/3 = 1 + 1.3333 + 1.6667 = 4. $$ 곱하는 수 1/3을 가중치라고 한다. 일반적으로 $$ \overline{x} = \frac{1}{n} \sum_{i=1}^{n} x_{i} = \left( \frac{1}{n} \right) x_{1} + \left( \frac{1}{n} \right) x_{2} + \cdots + \left( \frac{1}{n} \right) x_{n} $$ 1/n 은 가중치이고 모두 더하면 1이다.