6.4.3.6. 삼중 지수 평활법 예제
November 19, 2016
단일, 이중, 삼중 지수 평활법을 비교하는 예 이 예제에 있는 데이터를 통해 단일, 이중, 삼중 지수 평활법을 비교해보자.
다음 데이터에는 24개 관측값이 있다. 6년에 걸친 분기별 데이터이다(1년에는 4개의 분기가 있다).
| 연도 | 분기 | 시점 | 판매량 |
|---|---|---|---|
| 90 | 1 | 1 | 362 |
| 2 | 2 | 385 | |
| 3 | 3 | 432 | |
| 4 | 4 | 341 | |
| 91 | 1 | 5 | 382 |
| 2 | 6 | 409 | |
| 3 | 7 | 498 | |
| 4 | 8 | 387 | |
| 92 | 1 | 9 | 473 |
| 2 | 10 | 513 | |
| 3 | 11 | 582 | |
| 4 | 12 | 474 | |
| 93 | 1 | 13 | 544 |
| 2 | 14 | 582 | |
| 3 | 15 | 681 | |
| 4 | 16 | 557 | |
| 94 | 1 | 17 | 628 |
| 2 | 18 | 707 | |
| 3 | 19 | 773 | |
| 4 | 20 | 592 | |
| 95 | 1 | 21 | 627 |
| 2 | 22 | 725 | |
| 3 | 23 | 854 | |
| 4 | 24 | 661 |
단일, 이중, 삼중 지수 평활법으로 원본 데이터를 예측한 결과 그래프
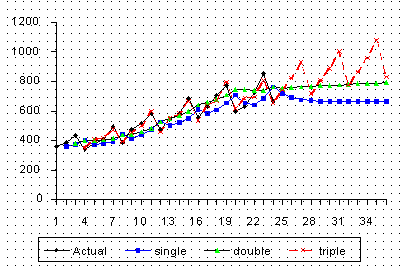가로축은 시점, 세로축은 판매량
삼중 지수 평활법으로 원본 데이터를 예측한 결과 그래프 실제 시계열과 예측치
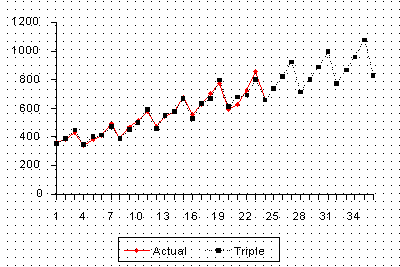가로축은 시점, 세로축은 판매량
MSE 비교
| MSE | \(\alpha\) 수요 | \( \gamma \) 추세 | \( \beta \) 계절성 |
|---|---|---|---|
| 6906 | 0.4694 | ||
| 5054 | 0.1086 | 1.0000 | |
| 936 | 1.0000 | 1.0000 | |
| 520 | 0.7556 | 0.0000 | 0.9837 |
위에서 계수 \( \alpha, \beta, \gamma \)는 각 기법마다 MSE를 최소화하는 프로그램으로 구한 것이다.
초기 추세 계산 예제
초기 추세 계산 데이터는 분기별 판매량 값으로 구성되어있다. 1년에 4개의 분기가 있기 때문에\( (L = 4) \) 계절은 1년이다. 위에서 구한 식을 사용하면, $$ \begin{align*} b_{1} &= \frac{1}{4} \left[ \frac{ y_{5}-y_{1} }{4} + \frac{ y_{6}-y_{2} }{4} + \frac{ y_{7}-y_{3} }{4} + \frac{ y_{8}-y_{4} }{4} \right] \\ &= \frac{1}{4} \left[ \frac{ 382-362 }{4} + \frac{ 409-385 }{4} + \frac{ 498-432 }{4} + \frac{ 387-341 }{4} \right] \\ &= \frac{5 + 6 + 16.5 + 11.5}{4} = 9.75 \end{align*} $$
초기 계절성 지표를 계산하는 예
초기 계절성 지표에 관한 표
| 분기 | 1번째 연도 | 2번째 연도 | 3번째 연도 | 4번째 연도 | 5번째 연도 | 6번째 연도 |
|---|---|---|---|---|---|---|
| 1 | 362 | 382 | 473 | 544 | 628 | 627 |
| 2 | 385 | 409 | 513 | 582 | 707 | 725 |
| 3 | 432 | 498 | 582 | 681 | 773 | 854 |
| 4 | 341 | 387 | 474 | 557 | 592 | 661 |
| \( \bar{X} \) | 380 | 419 | 510.5 | 591 | 675 | 716.75 |
이 예제에서 6년의 데이터를 사용했다. 다른 방법으로 하면 3이나 다른 값이 될 수도 있다. 초기값은 다양한 방법으로 계산할 수 있다.